- Pronouns
- he/him
- TNP Nation
- El_Fiji_Grande
- Discord
- El Fiji Grande (#3446)
Basics
You'll often hear that a vector has "both magnitude and direction." But what does this mean? Well, let's start by looking at one:
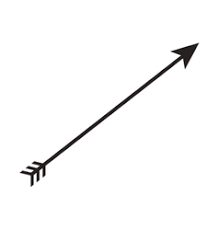The vector's length is proportional to its magnitude. The vector is pointing just about 45 degrees north of the horizontal. A good example of a vector is velocity. You could say that you're driving at 100 km/hr northeast, and this would give the information necessary to define the vector. The magnitude is the speed: the 100 km/hr. The direction is given as northeast.
Vectors are typically described in boldface. We could name the vector shown above as A. The magnitude of A can be denoted ||A||, or simply as A. The front of the vector can be referred to as the "tip," and the read of the vector can be referred to as the "tail."
Vector Addition
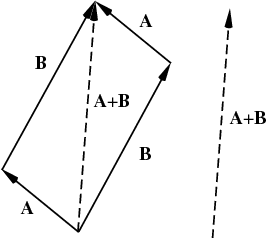
You can add vectors together! A good way to visualize the addition of two vectors is to draw them "tip-to-tail," by placing the tail end of the second vector at the tip of the first vector. The order in which this occurs does not matter; A+B = B+A. Drawing a line between the tail of the first vector and the tip of the relocated second vector results in a new vector, A+B. The new vector has its own magnitude and direction.
Vector Components
It can be helpful to break up a vector into its components relative to the Cartesian coordinate system. The Cartesian coordinate system has three principal axes: the x, y, and z axes, which are all perpendicular to each other.
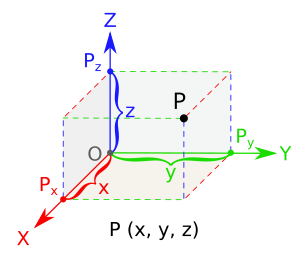
It is helpful to use a "right-handed" Cartesian coordinate system, as shown above. The origin is where the three axes intersect. In the image below, imagine a vector drawn from the origin to the point shown in 3-space. Let's name this vector D. This vector would have components in the x, y, and z directions as shown by the coordinates. These coordinates can be described as Dx, Dy, and Dz respectively. The coordinates are not bolded, as they describe only the magnitude of the components. To describe the direction, we define i^ to be in the x-direction, j^ to be in the y-direction, and k^ to be in the z-direction. Since the i^, j^, and k^ describe the direction, they are bolded. Technically, the ^'s should be shown directly over the i, j, and k, but zetaboards won't let me display those special characters. Together, we can fully describe vector D as D = Dxi^ + Dyj^ + Dzk^.
Vector Multiplication
There are two kinds of vector multiplication! There is the dot product and the cross product. The dot product is rather simple, and is defined as A.B = A*B*cos(theta), which results in a scalar quantity. Theta is the angle between the two vectors. The dot should be shown a bit above where it is, but that's just zetaboards being stupid again. Unlike the dot product (which results in a scalar), the cross product results in another vector. Simply put, AxB = A*B*sin(theta)*n^AB, where theta is the angle between vectors A and B, and n^AB is the unit (magnitude 1) vector normal (perpendicular) to the two vectors. This direction is defined by the right-hand-rule (RHR). Curl the fingers of your right hand from the first vector (A) to the second vector (B). The direction of your thumb will reveal the direction of n^AB.
You'll often hear that a vector has "both magnitude and direction." But what does this mean? Well, let's start by looking at one:
Vectors are typically described in boldface. We could name the vector shown above as A. The magnitude of A can be denoted ||A||, or simply as A. The front of the vector can be referred to as the "tip," and the read of the vector can be referred to as the "tail."
Vector Addition
You can add vectors together! A good way to visualize the addition of two vectors is to draw them "tip-to-tail," by placing the tail end of the second vector at the tip of the first vector. The order in which this occurs does not matter; A+B = B+A. Drawing a line between the tail of the first vector and the tip of the relocated second vector results in a new vector, A+B. The new vector has its own magnitude and direction.
Vector Components
It can be helpful to break up a vector into its components relative to the Cartesian coordinate system. The Cartesian coordinate system has three principal axes: the x, y, and z axes, which are all perpendicular to each other.
Vector Multiplication
There are two kinds of vector multiplication! There is the dot product and the cross product. The dot product is rather simple, and is defined as A.B = A*B*cos(theta), which results in a scalar quantity. Theta is the angle between the two vectors. The dot should be shown a bit above where it is, but that's just zetaboards being stupid again. Unlike the dot product (which results in a scalar), the cross product results in another vector. Simply put, AxB = A*B*sin(theta)*n^AB, where theta is the angle between vectors A and B, and n^AB is the unit (magnitude 1) vector normal (perpendicular) to the two vectors. This direction is defined by the right-hand-rule (RHR). Curl the fingers of your right hand from the first vector (A) to the second vector (B). The direction of your thumb will reveal the direction of n^AB.