How to calculate your nation's Gini Coefficient
This tutorial is also available on the NationStates forum here.
Some information about the Gini Coefficient (from Wikipedia):
The Gini Coefficient is the most commonly-used measurement for income equality in a region. It ranges from 0 to 1, or from 0% to 100%, with 0 indicating that everybody has the same amount of income and 1 indicating that one person earns all of the money in the region. While it can go above 1 when the lower end's income is negative (due to, for instance, massive piles of debt), that rarely happens.
The math behind the Gini Coefficient:
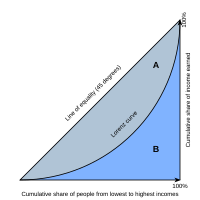X Axis: People, sorted from lowest to highest and accumulated. 0 is no population, 1 is all the population.
Y Axis: Income, sorted from lowest to highest and accumulated. 0 is no income, 1 is all the income.
Lorenz curve: The graph of a region's income dispersal.
Line of Equality: What the Lorenz curve would look like with perfect income equality.
A: The area between the Lorenz curve and the Line of Equality.
B: The area between the Lorenz curve and the axes.
The Gini coefficient is the ratio between the area A and the total area of the triangle A + B. Alternatively, since the triangle A + B has base and height of 1 (making the area 0.5), the Gini coefficient is equal to 2 * A.
The Formula
Disclaimer: As NationStates only provides so much information, your actual Gini coefficient would be higher than the one this formula provides you. However, this formula is as accurate as possible with the limited information provided.
First, go to your nation's Economy page. Toward the top, you should see something like this:
In red is your nation's average income, which will be called I from now on.
In green is your nation's poorest 10%'s average income, which will be called L from now on.
In blue is your nation's richest 10%'s average income, which will be called H from now on.
And finally, your Gini coefficient (as a percentage) is calculated as such:
Or, in text:
9 * (H - L) / I
For example, as is seen in the above Economy image, Darcania's average income is 42,060, its poorest average income is 30,760, and its richest average income is 55,500. Therefore:
H = 55,500;
L = 30,760; and
I = 42,060.
Thus, Darcania's Gini coefficient is:
9 * (55,500 - 30,760) / 42,060
which is equal to 5.29%.
How I derived this formula (Warning! Wall of text!):
Note: Not to scale.I started by determining a way to calculate the Gini coefficient from B instead of A, since B would have to be calculated either way:
G = A / (A + B)
G = (A + B - B) / (A + B)
A + B = 0.5
G = (0.5 - B) / 0.5
G = 1 - 2 * B
Next, some definitions:
LP = proportion of total income earned by lowest 10%
HP = proportion of total income earned by highest 10%
These will be calculated later.
Next, finding the area of B. Notice that B is composed of a triangle and two trapezoids; simply adding the areas of these three shapes will provide us with the area of B.
As a refresher, here are the formulas for calculating the areas of triangles and trapezoids:
Area of triangle = 0.5 * base * height
Area of trapezoid = 0.5 * height * (one base + second base)
And yes, I had to look up the area of a trapezoid. It's been too many years since elementary school.
Therefore:
B = 0.5 * 0.1 * LP + 0.5 * 0.8 * (LP + (1 - HP)) + 0.5 * 0.1 * ((1 - HP) + 1)
Next, since every term in right side of the equation had a factor of 0.5, I multiplied both sides by 2. Doing this now would eliminate an extra step later on, and allow us to plug in 2 * B directly into the formula for G above. I also factored out (but didn't eliminate) a factor of 0.1 to make simplification easier.
2 * B = 0.1 * (LP + 8 * (1 + LP - HP) + 1 + 1 - HP)
Distributing the 8 and combining like terms leads to:
2 * B = 0.1 * (9 * LP - 9 * HP + 10)
Distributing the 0.1 gives us the final formula for 2 * B:
2 * B = 1 + 0.9 * LP - 0.9 * HP
Substituting this result into the equation for G above produces:
G = 1 - (1 + 0.9 * LP - 0.9 * HP)
Distributing the minus sign, combining like terms, and factoring a 0.9 out leads to:
G = 0.9 * (HP - LP)
Next, we have to calculate what exactly HP and LP are, since they're not provided in the economy screen. Based off of the definitions of each of these terms, given above, we get:
LP = Total money earned by poorest 10% / Total money earned by population = 0.1 * population * L / (population * I)
Similarly, HP = 0.1 * population * H / (population * I)
Note that, for both terms, the population is in both the numerator and denominator, allowing us to cancel it out.
LP = 0.1 * L / I
HP = 0.1 * H / I
Plugging in these terms into the formula for G above results in:
G = 0.9 * (0.1 * H / I - 0.1 * L / I)
Factoring out 0.1 / I from both terms results in:
G = 0.09 * (H - L) / I
Finally, multiplying by 100 will give us G as a percentage:
G (as a percentage) = 9 * (H - L) / I
And now we have a formula for G using only easily-accessible numbers.
Feel free to ask any questions.
Enjoy knowing (and showing off) you nation's Gini coefficient!
Note: As a favor to me, when posting a Gini coefficient calculated using this method, please link to the NationStates forum post, as a way of crediting me and showing anyone who is curious how to calculate theirs. I spent quite a few hours working on this, and would enjoy any credit.
This tutorial is also available on the NationStates forum here.
Some information about the Gini Coefficient (from Wikipedia):
The Gini Coefficient is the most commonly-used measurement for income equality in a region. It ranges from 0 to 1, or from 0% to 100%, with 0 indicating that everybody has the same amount of income and 1 indicating that one person earns all of the money in the region. While it can go above 1 when the lower end's income is negative (due to, for instance, massive piles of debt), that rarely happens.
The math behind the Gini Coefficient:
Y Axis: Income, sorted from lowest to highest and accumulated. 0 is no income, 1 is all the income.
Lorenz curve: The graph of a region's income dispersal.
Line of Equality: What the Lorenz curve would look like with perfect income equality.
A: The area between the Lorenz curve and the Line of Equality.
B: The area between the Lorenz curve and the axes.
The Gini coefficient is the ratio between the area A and the total area of the triangle A + B. Alternatively, since the triangle A + B has base and height of 1 (making the area 0.5), the Gini coefficient is equal to 2 * A.
The Formula
Disclaimer: As NationStates only provides so much information, your actual Gini coefficient would be higher than the one this formula provides you. However, this formula is as accurate as possible with the limited information provided.
First, go to your nation's Economy page. Toward the top, you should see something like this:
In red is your nation's average income, which will be called I from now on.
In green is your nation's poorest 10%'s average income, which will be called L from now on.
In blue is your nation's richest 10%'s average income, which will be called H from now on.
And finally, your Gini coefficient (as a percentage) is calculated as such:
Or, in text:
9 * (H - L) / I
For example, as is seen in the above Economy image, Darcania's average income is 42,060, its poorest average income is 30,760, and its richest average income is 55,500. Therefore:
H = 55,500;
L = 30,760; and
I = 42,060.
Thus, Darcania's Gini coefficient is:
9 * (55,500 - 30,760) / 42,060
which is equal to 5.29%.
How I derived this formula (Warning! Wall of text!):
Note: Not to scale.
G = A / (A + B)
G = (A + B - B) / (A + B)
A + B = 0.5
G = (0.5 - B) / 0.5
G = 1 - 2 * B
Next, some definitions:
LP = proportion of total income earned by lowest 10%
HP = proportion of total income earned by highest 10%
These will be calculated later.
Next, finding the area of B. Notice that B is composed of a triangle and two trapezoids; simply adding the areas of these three shapes will provide us with the area of B.
As a refresher, here are the formulas for calculating the areas of triangles and trapezoids:
Area of triangle = 0.5 * base * height
Area of trapezoid = 0.5 * height * (one base + second base)
And yes, I had to look up the area of a trapezoid. It's been too many years since elementary school.
Therefore:
B = 0.5 * 0.1 * LP + 0.5 * 0.8 * (LP + (1 - HP)) + 0.5 * 0.1 * ((1 - HP) + 1)
Next, since every term in right side of the equation had a factor of 0.5, I multiplied both sides by 2. Doing this now would eliminate an extra step later on, and allow us to plug in 2 * B directly into the formula for G above. I also factored out (but didn't eliminate) a factor of 0.1 to make simplification easier.
2 * B = 0.1 * (LP + 8 * (1 + LP - HP) + 1 + 1 - HP)
Distributing the 8 and combining like terms leads to:
2 * B = 0.1 * (9 * LP - 9 * HP + 10)
Distributing the 0.1 gives us the final formula for 2 * B:
2 * B = 1 + 0.9 * LP - 0.9 * HP
Substituting this result into the equation for G above produces:
G = 1 - (1 + 0.9 * LP - 0.9 * HP)
Distributing the minus sign, combining like terms, and factoring a 0.9 out leads to:
G = 0.9 * (HP - LP)
Next, we have to calculate what exactly HP and LP are, since they're not provided in the economy screen. Based off of the definitions of each of these terms, given above, we get:
LP = Total money earned by poorest 10% / Total money earned by population = 0.1 * population * L / (population * I)
Similarly, HP = 0.1 * population * H / (population * I)
Note that, for both terms, the population is in both the numerator and denominator, allowing us to cancel it out.
LP = 0.1 * L / I
HP = 0.1 * H / I
Plugging in these terms into the formula for G above results in:
G = 0.9 * (0.1 * H / I - 0.1 * L / I)
Factoring out 0.1 / I from both terms results in:
G = 0.09 * (H - L) / I
Finally, multiplying by 100 will give us G as a percentage:
G (as a percentage) = 9 * (H - L) / I
And now we have a formula for G using only easily-accessible numbers.
Feel free to ask any questions.
Enjoy knowing (and showing off) you nation's Gini coefficient!
Note: As a favor to me, when posting a Gini coefficient calculated using this method, please link to the NationStates forum post, as a way of crediting me and showing anyone who is curious how to calculate theirs. I spent quite a few hours working on this, and would enjoy any credit.
